2166번: 다각형의 면적
첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을 넘지 않는 정수이다.
www.acmicpc.net
이 문제는 생각보다 쉬운데, 난 많이 돌아서 풀었다.
신발끈 공식을 적용하지 않은 풀이 방법이다.
1. 그냥 풀어 보았다
#include <iostream>
#include <vector>
#include <math.h>
struct Point
{
public:
int x;
int y;
};
std::vector<Point> dots;
int count;
// 2차원 평면공간서 두 점의 거리를 구합니다.
double getDistanceBetweenPoints(Point d1, Point d2)
{
return std::sqrt(std::pow((d2.x - d1.x), 2) +
std::pow(d2.y - d1.y, 2));
}
// 삼각형 3 변의 길이를 토대로 넓이를 리턴합니다.
double getHeronsFormula(double a, double b, double c)
{
double s = (a + b + c) / 2;
return std::sqrt(s * (s - a) * (s - b) * (s - c));
}
double getPolygonArea()
{
double area = 0;
for (int i = 1; i < count-1; ++i)
{
double distance1 = getDistanceBetweenPoints(dots[0], dots[i]);
double distance2 = getDistanceBetweenPoints(dots[i], dots[i + 1]);
double distance3 = getDistanceBetweenPoints(dots[i + 1], dots[0]);
area += getHeronsFormula(distance1, distance2, distance3);
}
return area;
}
int main()
{
std::cin >> count;
Point temp;
for (int i = 0; i < count; ++i)
{
std::cin >> temp.x >> temp.y;
dots.push_back(temp);
}
std::cout << getPolygonArea() << std::endl;
}원리는 간단하다.

2차원 공간상의 두 점이 주어지니, 해당 두 점의 거리를 getDistanceBetweenPoints() 함수를 통해 도출하고
이렇게 모든 두 점의 거리를 도출한 뒤 getHeronsFormula() 함수를 통해 헤론의 공식을 적용,
각 삼각형의 넓이를 구한뒤 이를 더하는 방식이다.
일반적인 형태의 정 다각형인 경우에 문제없이 잘 작동하나,
문제는 위와 같은 형태의 다각형만 존재하지 않는다는 점이다.
2. 문제가 되는 다각형

위와 같은 다각형 형태의 경우 내가 짠 코드를 실행시키면
ABC + ACD ... 를 통해
오목하게 들어간 부분의 값이 연속으로 '두번' 더해진다.
때문에 ABC * 2 분량의 오류가 생기며, 이러한 문제를 해결할 필요를 느끼고
결국 검색을 통해 문제를 해결하기로 하였다.
3. CCW
[알고리즘] CCW로 세 점의 방향성 판별하기
0. 들어가기 전에 첫 알고리즘 포스트입니다. 이번에 쓸 내용은 CCW입니다. 원래는 기하 알고리즘들을 전반적으로 다루려고 했는데 생각보다 글이 길어져서 CCW만 쓰게 되었습니다. 본 글의 내용
degurii.tistory.com
CCW 알고리즘을 이용하면 특정 점이 특정 선의 '시계방향' 에 위치하는지, '반시계방향' 에 위치하는지 판별할 수 있다.
도형의 넓이는 '음수' 가 나올 수 없으므로, 시계방향이던, 반시계 방향이던, 특정 방향을 '음수', 반댓방향을 '양수' 로 잡고
냅다 더한뒤에 std::abs() 함수를 이용해 절대값을 도출하면 최종적으로 도형의 넓이를 구할 수 있다고 생각했다.
4. 코드 수정
#include <iostream>
#include <vector>
#include <math.h>
struct Point
{
public:
int x;
int y;
};
std::vector dots;
int count;
// 2차원 평면공간서 두 점의 거리를 구합니다.
double getDistanceBetweenPoints(Point d1, Point d2)
{
return std::sqrt(std::pow((d2.x - d1.x), 2) +
std::pow(d2.y - d1.y, 2));
}
// 삼각형 3 변의 길이를 토대로 넓이를 리턴합니다.
double getHeronsFormula(double a, double b, double c)
{
double s = (a + b + c) / 2;
return std::sqrt(s * (s - a) * (s - b) * (s - c));
}
// ccw 값을 통해 point c 가 시계방향, 반시계 방향 중 어디에 존재하는지 리턴합니다.
int ccw(Point a, Point b, Point c)
{
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}
double getPolygonArea()
{
double area = 0;
for (int i = 1; i < count-1; ++i)
{
double distance1 = getDistanceBetweenPoints(dots[0], dots[i]);
double distance2 = getDistanceBetweenPoints(dots[i], dots[i + 1]);
double distance3 = getDistanceBetweenPoints(dots[i + 1], dots[0]);
if(ccw(dots[0], dots[i], dots[i + 1]) > 0)
{
area -= getHeronsFormula(distance1, distance2, distance3);
}
else
{
area += getHeronsFormula(distance1, distance2, distance3);
}
}
return std::abs(area);
}
int main()
{
std::cin >> count;
Point temp;
for (int i = 0; i < count; ++i)
{
std::cin >> temp.x >> temp.y;
dots.push_back(temp);
}
printf("%.1lf", getPolygonArea());
}CCW 의 원리를 알고 절대값 함수인 std::abs() 처리를 추가하였고,
문제를 다시 읽어본 결과 소수점 2자리수 까지만 return 하게 되어 있으므로 출력구문을 수정하였다.
GeoGebra 를 통해 실제 도형을 그리고 간단히 테스트 해 보았다.
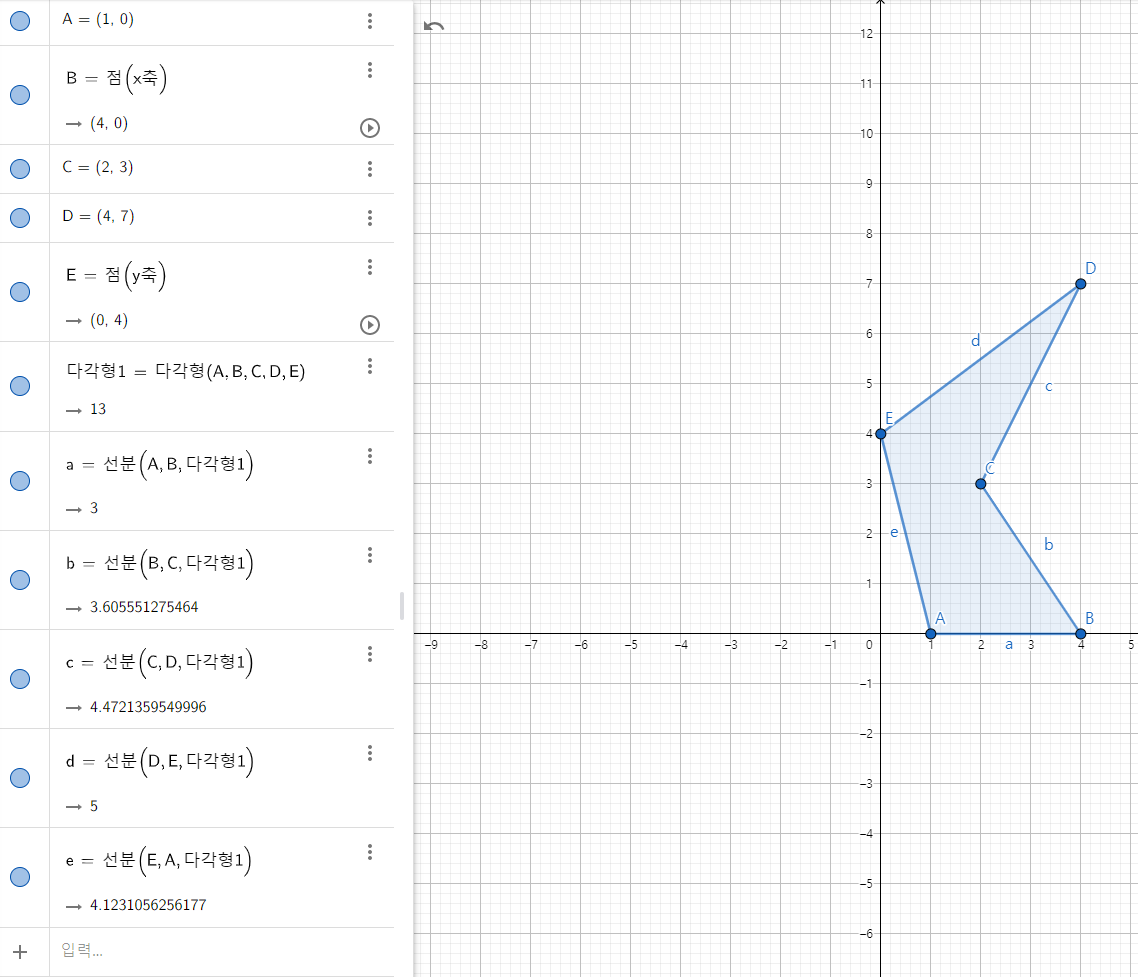
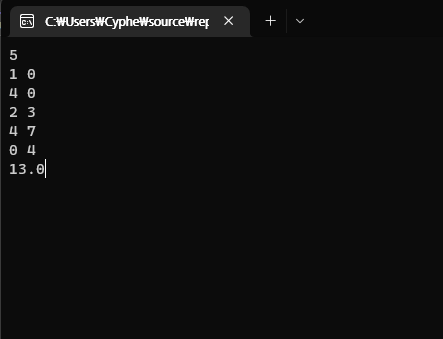
CCW if 문을 잘 타면서 올바르게 값을 도출하지만 최종적인 결과값은 '틀렸다' 고 도출되었다.
이유를 더 이상 찾을 수 없어 다른분들의 소스코드를 참조하였다.
5. 코드참조
[백준 2166] 다각형의 면적 (C++)
문제 링크: www.acmicpc.net/problem/2166 2166번: 다각형의 면적 첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을 넘지
imnotabear.tistory.com
해당 코드를 보면서 느낀점은 단순히 CCW는 Point 의 위치를 나타낼 뿐 만 아니라
CCW 자체를 활용해서 다각형의 '넓이' 를 도출해 낼 수 있다는 점이다.
CCW (Counter-ClockWise) - (2)
CCW (Counter-ClockWise) - (2) 이전 게시글 (CCW (Counter-ClockWise) https://wogud6792.tistory.com/10) 이번 게시글에서는 CCW알고리즘이 어떻게 이용되는지를 알아볼 것이다. 우선 CCW 알고리즘 코드는 다음..
rebro.kr
이를 '신발끈 공식' 이라고 지칭하는데
분명 어디서 들은거 같은데 기억이 안난다....
6. 내 방식이 틀린건 아니다. (다만 조금 비 효율적이다)
신발끈 공식을 몰랏기에, CCW를 활용해 도형의 넓이를 구하는 방식으로는 설계하지 못 하였다.
때문에 헤론의 공식을 통해 길이를 추출한 뒤, 삼각형별로 넓이를 구하고자 했고,
후에 문제점을 발견해 CCW를 활용, 보정하는 작업을 구성했다. (CCW만 사용하고, 신발끈 공식은 사용하지 않았다)
뇌피셜로는 틀림없이 넓이를 도출해 낼 수 있어야 하는데, '틀렸습니다' 는 왜 발생했을까???
imnotabear 님의 블로그 속 코드에서, 그 함정을 유추하고 문제를 다시 읽어보니 원인을 파악할 수 있었다.

'정수' 가 바로 함정이다.
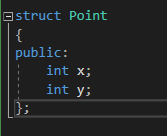
이 정수라는 명칭 때문에 나는 입력값으로 int 값을 사용 하였다. 가장 보편적으로 많이 사용되기 때문이고
100,000 이라는 MAX 수치는 int 형으로는 충분 해 보였다.
그런데 CCW 함수를 잘 살펴보면

입력 최대값인 100,000 * 100,000 = 10,000,000,000 백억으로 int 형의 최대값을 가뿐히 뛰어 넘는다.
리턴값은 입력값이 정수형이기에 굳이 double 형으로 리턴할 필요는 없었다. 때문에 Int 형을 쓴 것인데
이 부분에서 문제가 발생했다.
7. 최종코드
#include <iostream>
#include <vector>
#include <math.h>
struct Point
{
public:
long long x;
long long y;
};
std::vector<Point> dots;
int count;
// 2차원 평면공간서 두 점의 거리를 구합니다.
double getDistanceBetweenPoints(Point d1, Point d2)
{
return std::sqrt(std::pow((d2.x - d1.x), 2) +
std::pow(d2.y - d1.y, 2));
}
// 삼각형 3 변의 길이를 토대로 넓이를 리턴합니다.
double heronsFormula(double a, double b, double c)
{
double s = (a + b + c) / 2;
return std::sqrt(s * (s - a) * (s - b) * (s - c));
}
// ccw 값을 통해 point c 가 시계방향, 반시계 방향 중 어디에 존재하는지 리턴합니다.
long long ccw(Point a, Point b, Point c)
{
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}
double getPolygonArea()
{
double area = 0;
for (int i = 1; i < count - 1; ++i)
{
double distance1 = getDistanceBetweenPoints(dots[0], dots[i]);
double distance2 = getDistanceBetweenPoints(dots[i], dots[i + 1]);
double distance3 = getDistanceBetweenPoints(dots[i + 1], dots[0]);
// 사실상 음수, 양수중 어떤 쪽이든 abs() 를 취할것이므로 상관없다.
if (ccw(dots[0], dots[i], dots[i + 1]) > 0)
{
area -= heronsFormula(distance1, distance2, distance3);
}
else
{
area += heronsFormula(distance1, distance2, distance3);
}
}
return std::abs(area);
}
int main()
{
std::cin >> count;
Point temp;
for (int i = 0; i < count; ++i)
{
std::cin >> temp.x >> temp.y;
dots.push_back(temp);
}
printf("%.1lf", getPolygonArea());
}
ccw 함수의 리턴값과 Point x,y 값을 long long type 으로 수정하였다.

8. 결론
기초 공식의 원리와 쓰임새를 확실히 파악하자
기초적인 공식인 신발끈 공식도 모르는놈은 이런식으로 비 효율적인 코드를 짤 수 밖에 없다.
[백준 2166] 다각형의 면적 (C++)
문제 링크: www.acmicpc.net/problem/2166 2166번: 다각형의 면적 첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을 넘지
imnotabear.tistory.com
imnotabear 님의 코드를 보며
수학공식의 쓰임세를 정확히 알고 이를 적재적소에 적용하는것이 매우 중요한 것임을 다시한번 깨닫는다.
'Algorithm > BACKJOON' 카테고리의 다른 글
| [C++] 백준 15649 문제 해설 (0) | 2023.09.10 |
|---|---|
| [C++] 백준 1019 문제 해설 (0) | 2023.09.09 |
| [C++] 백준 1305 번 문제 해설 (0) | 2022.06.03 |
| [C++] 백준 19942 번 문제 풀이 (0) | 2021.08.08 |
| [C++] 백준 1009 번 문제 해설 (0) | 2021.07.18 |
