소개
신경망은 학습 데이터를 주면 손실을 출력한다. 이 때, 우리가 얻고 싶은것은 각 매개변수에 대한 '기울기$^{gradient}$' 이다. 바로 여기서 오차역전파법이 등장하고, 이 오차역전파법을 이해하기 위해서 연쇄법칙$^{chain\, rule}$ 을 알아야 한다. 연쇄법칙 자체는 어렵지 않다. 예로, 아래와 같은 함수가 둘 있다고 가정 해 보자.
$$ z = g(y) $$
$$ y = f(x) $$
이를 치환하면 $z = g(f(x))$ 가 되어, 최종 출력 $z$는 두 함수를 조합해서 계산할 수 있다. 이때 이 합성함수의 미분은 아래와 같이 구할 수 있다.
$$ {\partial z \over \partial x} = {\partial z \over \partial y} {\partial y \over \partial x} $$
$x$에 대한 $z$의 미분은 $y = f(x)$의 미분과 $z = g(y)$의 미분을 곱하면 구해진다. 그냥 이게 연쇄법칙의 전부이다. 연쇄법칙을 이용하면 신경망 내에 아무리 많은 함수를 연결해도 각 함수의 국소적인 미분을 구할 수 있고, 그 '국소적인' 미분값들을 곱해 '전체' 미분을 구할 수 있다.
실제 예제

위 그림에서는 좌측 → 우측 방향으로 순전파가 기재되어 있고. 우측 → 좌측 방향으로 역전파가 기재되어 있다. 위에서 언급했듯, 연쇄법칙을 이용하면 역전파의 미분값은, 출력쪽으로부터 흘러온 미분값과 각 연산 노드의 국소적인 미분을 곱해 계산할 수 있다. 그러므로 해당 예제에서는 아래와 같은 값을 도출할 수 있다.
$$ {\partial L \over \partial x} = {\partial L \over \partial z} {\partial z \over \partial x} $$
$$ {\partial L \over \partial y} = {\partial L \over \partial z} {\partial z \over \partial y} $$
덧셈노드의 역전파
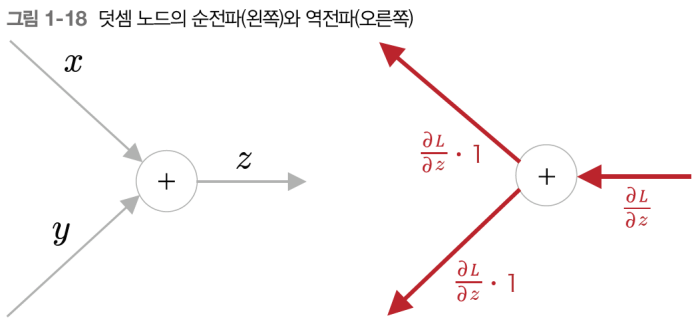
덧셈노드의 역전파는 단순히 출력값쪽에서 받은 값에 1을 곱하여 입력측으로 전파한다. 즉, 출력측으로부터 전달받은 기울기를 그대로 전달만 한다.
곱셈노드의 역전파

곱셈노드는 '출력측으로부터 받은 기울기' 에 '순전파 시의 입력을 서로 바꾼 값' 을 곱한다. 잘 보면 위에서 $x$, $y$ 가 서로 뒤바뀐걸 볼 수 있다.
분기노드의 역전파

단순히 복제하여 분기된다. 즉, 출력값측 노드로부터 전달된 기울기들의 '합' 이 된다.
+
3Blue1Brown 팀에서 제작한 Chain Rule 및 심층학습의 원리이다
인공지능을 배우는 분이라면 꼭 한번쯤 시청하길 권장한다.
'Artificial Intelligence > Basic' 카테고리의 다른 글
| 벨만 방정식(Bellman Equation) (0) | 2023.05.29 |
|---|---|
| 마르코프 결정 프로세스(Markov Decision Process) (0) | 2023.05.28 |
| 어텐션이란? (0) | 2023.04.14 |
| 점별 상호정보량(PMI, Pointwise Mutual Information) (0) | 2023.04.04 |
| 배치정규화 (0) | 2023.03.19 |