행렬 기초

이전 포스팅의 주제인 AdaLoRA 는 행렬에 대해 잘 알지 못하면 그 원리를 근본까지 이해하기 힘든 구성을 지니고 있다. 최종적으로 이해는 했지만 이를 정리해 두지 않으면 한달만 지나면 다 까먹을 것이기 때문에 기록해 둔다.

• 행렬
• 역행렬
• 전치행렬
• 대칭행렬
• 항등행렬(단위행렬)
• 대각행렬
• 직교행렬

및 행렬연산 특성에 관해서 설명한다.

 

 

1. 행렬(matrix)

$$\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$$

행렬에 관해서 모르는 사람은 없으리라 본다. Excel 을 다뤄본 경험이 있다면 행렬이란 계념을 추상적으로 잡아둔것과 다름없다.

벡터와 행렬의 차이에 관해 모르고 있었다면, 아래 글을 살펴보라.

Can anyone please explain the the difference between a vector and a matrix?

 

 

1-1. 행렬의 덧셈, 뺄셈

행렬의 덧셈과 뺄셈은 따로 설명이 필요하지 않을 정도로 간단하다.
같은 크기를 지닌 행렬끼리만 덧셈, 뺄셈 연산이 가능하다.

import numpy as np

matrix_a = np.array([[1,2,3],
                   [4,5,6],
                   [7,8,9]])

matrix_b = np.array([[9,8,7],
                   [6,5,4],
                   [3,2,1]])


print(matrix_a + matrix_b)
print(matrix_a - matrix_b)

$$A+B=\left[\begin{array}{ccc}10& 10& 10\\ 10& 10& 10\\ 10& 10& 10\end{array}\right]$$

$$A-B=\left[\begin{array}{ccc}-8& -6& -4\\ -2& 0& 2\\ 4& 6& 8\end{array}\right]$$

 

1-2. 행렬의 곱셈

행렬곱 역시 특정 조건을 갖춘 행렬간에만 수행할 수 있다.
예로, 두 행렬 $A,B$가 각각 $m\times n,n\times r$일 때 진행할 수 있다.
앞쪽에 위치하는 행렬 $A$의 열의 수와, 뒤쪽에 위치하는 행렬 $B$의 행의 수가 같아야 한다.

행렬끼리 곱셈 연산을 수행하면 행렬의 크기는 $m\times r$이 된다.

import numpy as np

matrix_a = np.array([[80,90,60],
                   [75,80,90],
                   [90,95,65],
                   [99,70,70]])

matrix_b = np.array([[3,1],
                   [3,8],
                   [4,1]])


print(np.dot(matrix_a, matrix_b))

예로, 위와 같은 코드가 있다면 아래와 같이 계산된다.

$$AB=\left[\begin{array}{cc}80\cdot 3+90\cdot 3+60\cdot 4& 80\cdot 1+90\cdot 8+60\cdot 8\\ 75\cdot 3+80\cdot 3+90\cdot 4& 75\cdot 1+80\cdot 8+90\cdot 8\\ 90\cdot 3+95\cdot 3+65\cdot 4& 90\cdot 1+95\cdot 8+65\cdot 8\\ 99\cdot 3+70\cdot 3+70\cdot 4& 99\cdot 1+70\cdot 8+70\cdot 8\end{array}\right]=\left[\begin{array}{cc}750& 860\\ 825& 805\\ 815& 915\\ 787& 729\end{array}\right]$$

몇번 보다보면 계산법을 쉽게 찾을 수 있다. 앞 행렬에 해당하는 $A$의 행과, 뒷 행렬에 해당하는 $B$의 열과 곱하면 된다. 이 때 행, 열의 요소가 여러개일 때에는 각 곱 계산을 더한다.

참고로 행렬곱에서 교환법칙은 대부분 성립하지 않는다. (특수한 경우 성립하나, 일반적으로 성립 X)

$$AB\ne BA$$

 

 

 

2. 역행렬(inverse matrix)

역행렬(inverse matrix) 는 행렬 $A$가 있다고 할 때 $A^{-1}$로 표기되며, 아래가 성립된다.

$$A^{-1}A=A{A}^{-1}=I$$

여기서 $I$는 '단위 행렬(unit matrix)' 혹은 '항등 행렬(identity matrix)' 이라고 불리며, 아래에서 설명하겠다.

 

역행렬은 항등행렬을 구하기 위해 사용된다. 

 

 

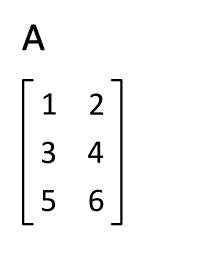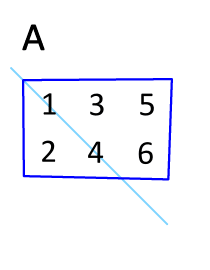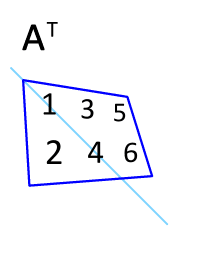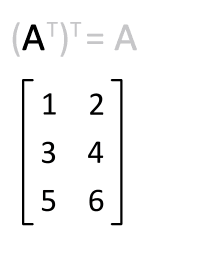
3. 전치행렬(transposed matrix)

행렬 $A$의 전치행렬을 표기할 때 $A^T$ 혹은 $A^{\mathrm{\top }}$ 으로 표기된다.(나는 $A^{\mathrm{\top }}$표기를 선호한다.)
전치행렬은 행렬내의 원소를 대각선축을 기준으로 서로 위치를 바꾼것을 의미한다.

즉, $A$가 $m\times n$ 이라면 $A^{\mathrm{\top }}$은 $n\times m$ 이다.

전치행렬은 아래 특성이 성립된다.

$$A^{\mathrm{\top }\mathrm{\top }}=A$$

 

 

 

4. 대칭행렬(symmetric matrix)

행렬 $A$가 아래 조건을 만족한다면 대칭행렬 이라고 지칭한다.

$$A=A^T$$

따라서 $A_{ij}=A_{ji}$ 역시 성립한다.

 

또한 아래의 성질도 보유하고 있다. ($n$차 정사각행렬 이라면)

$$\text{대칭행렬}=A{A}^{\mathrm{\top }}=A^{\mathrm{\top }}A$$

 

예로, 아래는 대칭행렬이다.

$$\left[\begin{array}{ccc}1& 2& 4\\ 2& 3& 5\\ 4& 5& 6\end{array}\right]$$

1, 3, 6 이 위치한 대각선축을 따라 전치해도 같은 행렬이 된다는 것을 알 수 있다. 

 

 

 

5. 항등행렬(unit matrix)

항등행렬(단위행렬) 은 주대각선의 원소가 모두 1이며, 나머지 원소는 모두 0인 정사각 행렬을 의미한다.

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

 

 

 

6. 대각행렬(main diagonal)

주대각선에 위치한 행렬을 제외한 모든 성분이 0인 정사각 행렬을 말한다.

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 8& 0\\ 0& 0& 3\end{array}\right]$$

 

 

7. 직교행렬(orthogonal matrix)

직교행렬은 아래와 같은 특성을 지닌다.

• $A^{\mathrm{\top }}=A^{-1}$
• $A^{\mathrm{\top }}A=A{A}^{\mathrm{\top }}=I$

위에서 역행렬과 원본행렬을 곱하면 항등행렬이 된다고 언급했었다. 하지만 직교행렬의 경우 역행렬과 전치행렬이 개념상 같으므로, 전치행렬과 행렬원본을 곱해도 항등행렬이 도출된다. 즉 아래와 같다.

•  $A^{\mathrm{\top }}A=A^{-1}A$

 

아래의 예제를 살펴보자.

$$A=\left[\begin{array}{cc}\cos (x)& \sin (x)\\ -\sin (x)& \cos (x)\end{array}\right]$$

$$A^{\mathrm{\top }}=\left[\begin{array}{cc}\cos (x)& -\sin (x)\\ \sin (x)& \cos (x)\end{array}\right]$$

$$A{A}^{\mathrm{\top }}=\left[\begin{array}{cc}{\cos }^2(x)+{\sin }^2(x)& -\cos (x)\sin (x)+\sin (x)\cos (x)\\ -\sin (x)\cos (x)+\cos (x)\sin (x)& {\sin }^2(x)+{\cos }^2(x)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=I$$

 

파이썬 예제 코드를 통해 위 예제의 출력값을 확인해 보자.

import numpy as np
import math

x = 3.141592

A = np.array([[math.cos(x),      math.sin(x)],
			  [math.sin(x) * -1, math.cos(x)]])

At = np.array([[math.cos(x),    math.sin(x) * -1],
              [math.sin(x),    math.cos(x)]])

print(np.dot(A, At))

$$A{A}^{\mathrm{\top }}=\left[\begin{array}{cc}1.00000000e+00& -4.32611126e-23\\ -4.32611126e-23& 1.00000000e+00\end{array}\right]$$

프로그래밍 언어 특성상 부동소수점 오차 문제로 완벽히 0이 도출되진 않으나, 항등행렬을 띔을 알 수 있다.