[리뷰] AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning

해당 논문은 LoRA 를 개선한 버전인 AdaLoRA 에 대해 제안하는 논문이다.

 

1. 서론

기존 Full Fine-Tuning, LoRA 는 NLP 에서 중요한 패러다임이 되었으나, 일반적으로 '모든' parameter 를 미세 조정하기에 최적의 조정을 수행할 수 없다는 단점이 있다.

이러한 문제를 해결하기 위해 가중치 행렬 간 parameter 자원(budget) 을 중요도 점수에 따라 적응적으로 할당하는 AdaLoRA 를 제안한다. 특히 AdaLoRa 는 특이값 분해(Singular Value Decomposition, SVD)의 형태로 증분 업데이트를 parameter 화 한다. 이러한 접근 방식을 통해 중요하지 않은 업데이트의 특이값을 효과적으로 가지치기할 수 있으며, 이는 본질적으로 parameter 의 필요 자원을 줄이는 역할을 할 수 있다.

마지막으로 논문에서는 AdaLoRA 의 효과를 검증하기 위해 여러 광범위한 실험을 수행한다. 특히 AdaLoRA 가 저예산 환경에서 매우 큰 개선을 보여준다는 점을 확인할 수 있다.

 

2. 소개

논문 저자들은 모든 가중치 행렬을 업데이트 하는 것 보다 일부 가중치 행렬만 수정하는것이 더 높은 성능을 달성한다는것을 발견하였다.

그림 1: 학습 가능한 총 매개 변수가 0.28M인 경우 DeBERTaV3 기반의 선택된 가중치 행렬(왼쪽) 또는 선택된 레이어(오른쪽)에만 LoRA를 적용하고 MNLI-m의 미세 조정 성능을 비교한다. 그림 (a): 쿼리/키/값 투영($W_q$, $W_k$, $W_v$), self-attention 출력 투영($W_o$), 2 layer FFN의 두 가중치 행렬($W_{f1}$, $W_{f2}$)을 포함하여 모든 Transformer 레이어의 선택된 유형의 가중치 행렬만 미세 조정한다. 그림 (b)에서는 선택된 레이어의 모든 가중치 행렬에 LoRA를 적용한다.

이는 모든 가중치 행렬을 조정하는것이 최적이지 않다는 것을 의미한다. 즉 optimal 하지 않다. 그렇다면 어떤 가중치 행렬, 어떤 레이어를 선택해야지 가장 optimal 한 업데이트를 수행할 수 있을까?

즉.

어떻게 PEFT 의 성능을 향상시키기 위해,
모듈의 중요도에 따라 parameter 의 자원을 적응적으로 할당 할 수 있을까?

 

이 질문에 대한 답으로 저자들은 AdaLoRA 를 제안한다.

AdaLoRA 는 자원을 제어하기 위해 incremental matrices(증분행렬) 의 rank 를 조절한다. 중요한 증분행렬이라면 보다 세분화된 작업별 정보를 잘 캐치할 수 있도록 높은 rank 로 할당된다. 반면 덜 중요하다면 과적합 예방, 및 예산을 절약하기 위해서 낮은 rank로 할당할 수 있다.

그림 3: AdaLoRA로 MNLI를 기반으로 DeBERTaV3 기반 미세 조정 시 각 증분 행렬의 결과 순위. 여기서 x축은 레이어 인덱스이고 y축은 다양한 유형의 적응된 가중치 행렬을 나타낸다.

기존 연구에서는 행렬의 rank를 제어하는 여러 방법들이 제안되었으며, 대부분은 행렬의 특이값 분해(SVD)를 직접 계산하여 가장 작은 특이값을 가지치기한다. 이러한 연산은 rank를 명시적으로 조작할 수 있게 만들며, 결과 행렬과 원래 행렬 간의 차이를 최소화한다.

그러나 대규모 모델을 미세 조정할 때는 이러한 연산이 고차원 가중치 행렬에 대해 반복적으로 SVD를 적용하는 것이 매우 비효율적이다.(SVD의 연산량은 정사각 행렬일 경우 $O(n^3)$ 이다.) 그래서 AdaLoRA는 실제 SVD를 계산하는 대신에 $A = P \Lambda Q$ 로 행렬 $A$ 를 파라미터화 하여 SVD 를 모방한다. 여기서 대각행렬 $\Lambda$ 는 특이값을 포함하고, 직교하는 행렬 $P$ 와 $Q$는 $A$의 좌우 특이 벡터를 대표한다.   

이런 파라미터화를 통해 SVD의 계산량이 많은 부분을 피할 수 있고, 또 다른 이점으로 중요하지 않은 특이값을 감소시키면서도, 그렇지 않은 벡터는 유지시킬 수 있기에 전체적인 훈련과정을 안정화 시킬 수 있다.

결론적으로 AdaLoRA 는 SVD를 모방한 방식을 기반으로한 새로운 LoRA 방법으로, 가중치 행렬 $A$ 의 rank 를 중요도에 따라 동적으로 조정한다. 증분행렬 $P \Lambda Q$ 를 중요도 점수에 의해 세 개의 그룹으로 나누고, 이러한 중요도는 모델 성능에 기여하는 정도에 따라 측정된다. 중요도가 낮은 특이값은 가지치기되어 계산 절약, 과적합 방지에 기여하며, 중요한 특이값은 미세 조정을 위해 보존된다.

 

2-1. SVD

SVD는 선형대수학에서 중요한 계념중 하나이다. 임의의 행렬을 특정 구조의 세가지 행렬의 곱으로 분해하는것을 말한다. 이는 $A = U \Sigma V^\top$ 로 표현되는데,

• $A$ : $m \times n$ rectangular matrix
• $U$ : $m \times m$ orthogonal matrix
• $\Sigma$ : $m \times n$ diagonal matrix
• $V$ : $n \times n$ orthogonal matrix

이다.

참고로 여기서 중요하게 여겨지는 성질이 아래와 같다. $U$ 가 행렬이라고 할 때

$$
\begin{gather}
UU^\top = U^\top U = I\\
U^{-1} = U^\top
\end{gather}$$

이 성립한다. (이 원리를 이용해 AdaLoRA 에 핵심적인 원리가 구동된다.)

이러한 SVD 기술을 사용함으로서 AI 분야에서는 아래와 같은 장점을 얻을 수 있다.

• 데이터 압축, 차원 축소
• 잠재 의미 분석
• 모델 파라미터 정규화
• 네트워크의 복잡도 감소

특이값 분해(SVD) - 공돌이의 수학정리노트 (Angelo's Math Notes)

최종적으로 SVD는 임의의 행렬 A를 정보량에 따라 여러 layer로 분할하기 위해서 사용된다.

 

3. AdaLoRA Method

3-1. SVD-Based Adaptation

위에서 언급된 바와 같이, AdaLoRA 는 pre-trained 가중치 행렬의 증분 업데이트를, 특이값 분해 형태로 매개변수화 한다.

$$\large {W = W^{(0)} + \Delta + W^{(0)} + P \Lambda Q}$$

$P\in\mathbb{R}^{d_1\times r}, Q\in\mathbb{R}^{r\times d_2}$는 각각 left, right singular vector 를 나타내고, $\Lambda\in\mathbb{R}^{r\times r}$ 는 singular value 를 대각행렬로 가지며, 대각행렬 $\Lambda$는 특이값 $\{\lambda_i\}_{1\leq i\leq r}$ 를 포함하며, rank $r$ 은 $r\ll min(d_1,d_2)$ 값을 지닌다. (즉 $d_1, d_2$ 의 최소값보다 작다)

이는 LoRA와 비교시 $\Lambda$ 의 $r$ 차원의 벡터만 추가된 것이다. 예로, LoRA 논문의 4.1 Low-Rank-Parametrized Update Matrices 를 살펴보면 아래와 같은 내용을 살펴볼 수 있다.

사전 훈련된 가중치 행렬 $W_0 \in \mathcal{R}^{d \times k}$ 의 업데이트를 제한하기 위해, row-rank 분해를 $W_0 + \Delta W = W_0 + BA$ 로 표현한다. 여기서 각 기호는 다음과 같은 의미를 지닌다. $B \in \mathcal{R}^{d \times k}$, $A \in \mathcal{R}^{r \times k}$, 그리고 rank $r$ 은 $r \ll min(d, k)$ 값을 가진다.

훈련중 $W_0$ 는 동결되며, 기울기 업데이트를 받지 않는다. 반면 $A, B$ 는 trainable parameters 이다. $W_0$ 와 $\Delta W = BA$ 는 모두 동일한 입력값으로 곱해진다.

따라서 LoRA 는 아래와 같은 수식을 지닌다.

https://medium.com/@lokeshtodwal/demystifying-lora-q-lora-ea267abff48

$$h = W_0x + \Delta W x = W_0 x + BA x$$

여기서 $A \in \mathbb{R}^{r \times k}$, $B \in \mathbb{R}^{d \times r}$ 이므로, AdaLoRA 와 비교하면 $P \Lambda Q$ 와 비교해야 하는데, $P\in\mathbb{R}^{d_1\times r}, Q\in\mathbb{R}^{r\times d_2}$ 로 상쇄되고, 결국 $\Lambda$ 만 남으로므로 $r$ 차원의 벡터만 하나 추가됨 셈이다. 때문에 이런 의문을 가질 수 있다.

그냥 고전적인 LoRA 에서 $A$, $B$ 를 가지치기 하면 되는거 아닌가? AdaLoRA 가 이것과 무슨 차이가 있는데?

이 질문에 대해서 저자들은 아래와 같이 답변한다.

• 만약 $A,B$ 를 제거 하였을 때, 그것을 다시 활성화 하는것은 불가능하다.
  반면 AdaLoRA 는 $\Lambda$ 중 하나를 0으로 변경만 하는것이기에 원래 rank 를 얼마든지 활용 가능하다.(0으로 곱해서 제거하는 방식이기에 충분히 복구할 수 있는 방식.)
• $A, B$는 서로 직교하지 않으므로, 이를 수정한다면 다른 영역에 영향을 줄 수 있다.

 

더하여 SVD를 계산하기 위해 모든 $\Delta$ 에 SVD 를 직접 계산할 수 있으나, 위에서 언급하였듯 계산 복잡성은 $O(min(d_1, d_2)d_1 d_2)$ 이다.(정사각 행렬일 경우 $O(n^3)$) 여기서 $d_1$ 과 $d_2$ 는 행렬이므로, 커질수록 계산 비용이 크게 늘어난다. 때문에 아래와 같은 수식을 사용하여 $P$(왼쪽 특이 벡터)와 $Q$(오른쪽 특이 벡터) 가 얼마나 직교행렬에 가까운지 체크하며(SVD의 특징을 모방하기 위해), 동시에 아래와 같은 정규화를 사용한다. 

$$ \large{R(P, Q) = ||P^\top P - I||_F^2 + ||QQ^\top - I||_F^2} $$

• $R$ : 정규화 항으로서 $P, Q$ 가 직교행렬이 되도록 하는 역할을 한다.
• $F$ : Frobenius Norm (벡터의 L2 lorm 을 행렬로 확장한 것으로 볼 수 있다.)
• $\top$ : 전치 행렬로서, 행렬의 행과 열이 서로 바뀐 행렬을 의미한다.
• $P^\top P$ 및 $QQ^\top$ : 이런식으로 각 행렬의 전치를 곱한다는 의미는 대칭행렬을 만든다는 의미이다.
• $I$ : 항등행렬을 의미한다.
• $P^\top P - I$ 와 $QQ^\top - I$ : 이를 수행함으로서 항등행렬 $I$ 에 더 가깝게 되도록 만든다. 이를 통해 $P, Q$를 직교행렬이 되도록 유도한다.

이를 통해 점진적으로 업데이트 해 가며 SVD와 비슷한 효과를 낼 수 있다.

직교 행렬은 전치 행렬과 곱하였을때 항등행렬인 $I$를 생성한다. 결국 위 수식에서 $P^\top$, $P$ 그리고 $Q^\top$, $Q$가 각각 항등행렬에서 얼마나 차이가 나는지를 제곱함으로서 측정한다. 이 최종 값이 더 작아질수록 $P$와 $Q$는 더 직교에 가까워진다.

직교행렬의 전치행렬은 역행렬과 같다. 따라서 $P^{\top} = P^{-1}$ 그리고 $Q^{\top} = Q^{-1}$ 이다. 때문에 직교행렬을 자신의 전치행렬과 곱하면 항등행렬 $I$가 된다. 결국 $Q$ 가 직교행렬일때, $Q \times Q^\top = I$ 가 성립한다. 따라서 AdaLoRA 에서 $P^\top P$ 와 $QQ^\top$ 이 항등행렬 $I$ 에 가깝게 만드는것은 $P$와 $Q$ 가 직교행렬이 되도록 유도한다는 것과 같은 의미가 된다.

더하여 '더 작아질수록' 이라는 말에 집중해 보면, 결국 필요없는 부분을 '점진적으로' 제거해가며 이 최종 값을 작아지도록 만들 수 있는 것이다. $P^\top P$, $QQ^\top$ 값이 항등행렬 $I$ 에 가까워질수록 0에 가까워진다.

 

 

3-2. Importance-aware Rank Allocation

위에서 $P$와 $Q$ 에 대해서 어떻게 최적의 값을 찾는지 알아 보았다면, 해당 섹션에서는 $\Lambda$ 값을 어떻게 조정하는지 알아본다.

LoRA 와 비교해서 $\Lambda$ 에 해당되는 $r$차원의 벡터의 차이가 바로 AdaLoRA 의 차이였다. 때문에 $\Lambda$ 값은 AdaLoRA 에 있어서 핵심이라고 할 수 있으며, $\Lambda$를 통해 어떤 가중치 행렬을 얼마나 더 업데이트할지 정한다. 

---

저자들은 $W_q, W_k, W_v, W_{f1}, W_{f2}$ 를 포함한 모든 transformer 가중치 행렬에 SVD기반 adaptation(어떤걸 냅두고, 어떤걸 가지치기 할 것인지 조정하는것을 뜻함) 적용하였다. 이때 명확한 참조를 위해 증분행렬 $k$를 색인(index) 한다.

$$ \large{\Delta k = P_k \Lambda_k Q_k \quad \text{for} \, k = 1, \cdots n}$$

$P_k, \Lambda_k, Q_k$ 는 각각 왼쪽 특이벡터, 특이값, 오른쪽 특이 벡터이며, $n$ 은 adapted weight matrices 의 수이다.
최종적으로 아래와 같은 수식을 통해 스탭$t$에 대해 stochastic gradient 를 구할 수 있다.

$$\tilde\Lambda_k^{(t)}=\Lambda_k^{(t)}-\eta\nabla_{\Lambda_k}\mathcal{L(P,E,Q)}$$

 

아래는 수식에 대한 직접적인 설명이다.

• $\tilde\Lambda_k^{(t)}$ : 시간단계 $t$에서의 증분행렬 $k$(특이값이 수정된 상태)
• $\Lambda_k^{(t)}$ : 시간단계 $t$에서의 증분행렬 $k$(특이값이 수정되지 않은 상태)
• $\nabla_{\Lambda_k}\mathcal{L(P,E,Q)}$ : training objective(손실함수의 대분류) $\mathcal{L(P,E,Q)}$ 에 대한 $\nabla_{\Lambda_k}$ 의 기울기
• $\eta$ : learning-rate

 

아래는 수식에 대한 참고 내용이다.

• $\Delta k$의 $i$번째 트리플렛을 $\mathcal{G}_{k,i} = {P_{k, *i}, \lambda_{k,i}, Q_{k,i*}}$ 로 표시(증분행렬 $k$에서  $P_{k, *i}$는 $i$번째 왼쪽 특이벡터,  $\lambda_{k,i}$는 $i$번째 특이값,  $Q_{k,i*}$는 $i$번째 오른쪽 특이 벡터)
• 중요도 점수를 $S_{k,i}$ 로 표시.
• 매개변수 집합 $\mathcal{P}=\{{P_k}\}_{k=1}^{n}, \mathcal{E} = \{\Lambda_k\}^n_{k=1}, \mathcal{Q} = \{ Q_k \}^n_{k=1}$ 의 훈련비용을 $\mathcal{C(P, E, Q)}$ 로 표기.
• 정규화과정($R(P, Q)$)의 경우, 훈련 목표는 $\mathcal{L(P, E, Q) = C(P, E, Q)} + \mathcal{\gamma \Sigma^n_{k=1}} R(P_k, Q_k)$($\gamma > 0$는 정규화 계수)

---

아래 수식은 특이값 분해에서 행렬 $\Lambda_k^{(t+1)}$ 을 계산하는 과정을 나타낸다. $\mathcal{T}$ 는 임계값 함수로, 중요도 점수 $S_k^{t}$ 에 따라 가장 중요한 상위 $b^{(t)}$ 개의 특이값을 유지하고, 나머지는 0로 설정하는 역할을 수행한다

$${\Lambda}_k^{(t+1)} = \mathcal{T}(\tilde{\Lambda}_k^{(t)}, S_k^{(t)}), \text{ with } \mathcal{T}(\tilde{\Lambda}_k^{(t)}, S_k^{(t)})_{ii} = 
\begin{cases} 
\tilde{\Lambda}_{k,ii}^{(t)} & \text{if } S_{k,i}^{(t)} \text{ is in the top-}b^{(t)} \text{of } S^{(t)}, \\
0 & \text{otherwise}.
\end{cases}
$$

이하 수식에 대한 설명은 아래와 같다.

• $t$ : 시간단계
• $b$ : 가지치기 단계에서 특이값 중 중요도가 높은 상위 몇 개를 유지할지 결정하는 값. 즉 특정 시간단계$(t)$ 에 대한 limit 값, 예산(budget), 자원을 의미한다.
• $k$ : 각 트랜스포머 레이어의 가중치 행렬, $1 \sim n$ 값을 가지며, $n$은 레이어에 있는 가중치 행렬의 총 수임.
• $i$ : 특정 가중치 행렬 $\Delta$k 의 특이값 중 하나를 나타내는 인덱스.
• $S_{k, i}^{(t)}$ : 특정 시간단계 $t$에서 증 행렬 $k$의, $i$번째 트리플렛의 중요도.
• $\tilde{\Lambda}_k^{(t)}$ : 특정 시간단계$t$에서 $k$번째 증분 행렬에 대한 저차원 근사치에서 파생된 특이값을 포함하는 행렬. 해당 행렬은 SVD를 통해 얻은 결과의 일부이며, 가중치 행렬 $W$를 저차원 공간으로 근사하는데 이용.
• $\tilde{\Lambda}_{k,ii}^{(t)}$ : $k$ 번째 증분 행렬의 $i$ 번째 특이값에 해당행렬에 대한 정보를 담고있음. 중요도에 기반해 가지치기 과정을 통하여, 해당 특이값중 일부는 다음 시간 단계에서 유지되거나, 아예 제거될 수 있음.

이를 통해 중요도가 낮은 정보는 제하고, 중요한 특성을 갖는 특이값을만 보존하여 다음 단계의 훈련에 사용함으로서, 계산 효율성을 높이는데 도움을 준다.

 

최종적으로 AdaLoRA 는 아래와 같은 과정을 따른다.

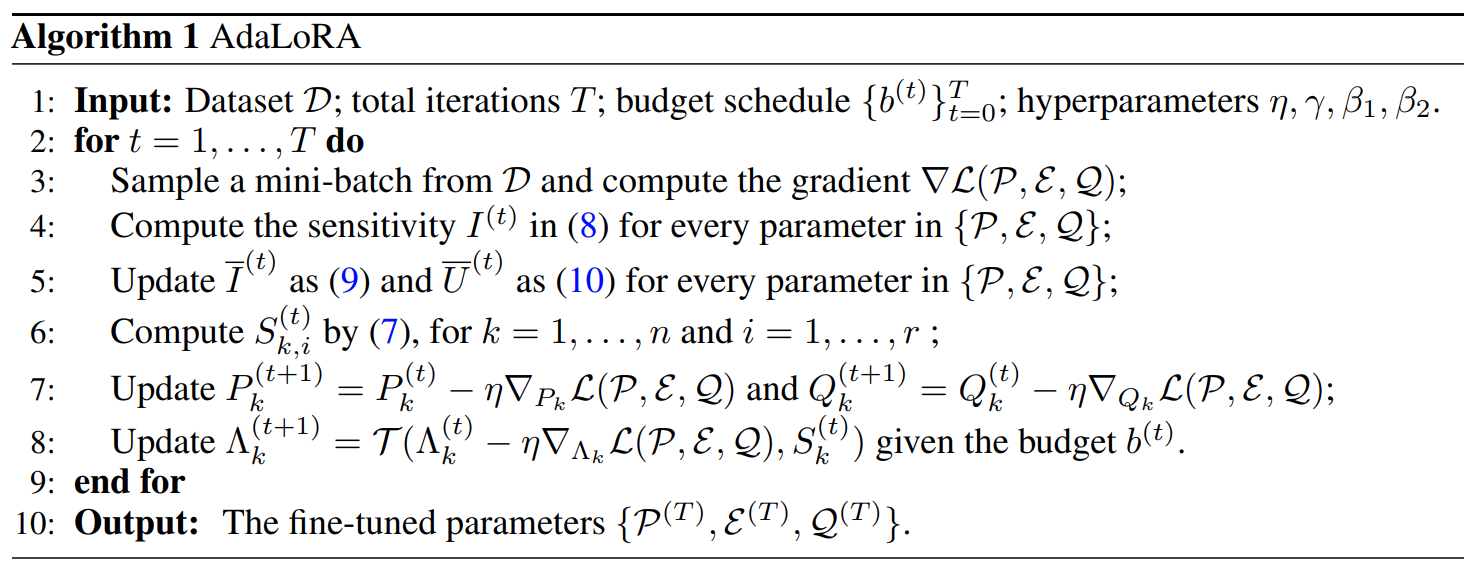
간단히 요약하면 아래와 같다.

$\bar{I}^{(t)}$, $\bar{U}^{(t)}$ 는 각각 민감도(파라미터가 얼마나 민감한가, 작은 변화가 얼마나 큰 영향을 미치는가(다만 지수이동 평균을 통해 smoothing 되어있음))와, 정량화된 불확실성($I^{(t)}$와 $\bar{I}^{(t)}$ 사이의 국부적 변동에 의해 정량화된 불확실성, 민감도의 추정치가 얼마나 정확한가, 불확실성이 높다면 민감도 추정치를 조심히 다뤄야함)을 의미함.

• 데이터셋에서 미니배치 샘플링, 해당 배치에 대한 기울기를 계산.
• 파라미터에 대해 민감도, 중요도를 갱신한다.
• 이를 통해 $P, Q$ 와 특이값 $\Lambda$ 를 업데이트한다.
• 이를 반복-파라미터를 조절한다.
• 최종적으로 미세 조정된 파라미터를 출력한다.

 

결국, LoRA 와 AdaLoRA 의 차이는

AdaLoRA 는 중요도를 기반으로 가중치를 업데이트 할 수 있다. LoRA 는 모든 파라미터에 대해 동일 업데이트 적용하지만 AdaLoRA 는 특이값의 중요도를 평가하기에, 더 중요한 파라미터에 더 많은 '자원(budget)'  을 할당할 수 있으며, 상대적으로 중요하지 않은 파라미터의 가중치 행렬을 점진적으로 제거하여 과적합 방지, 일반화 성능 향상 등에 기여한다.

 

3-3. Global Budget Scheduler

rank 를 조정하는 이유는, low-rank adaptive 맥락에서 매개변수의 예산을 제어하기 위해서이다. 이러한 예산의 조절은 미세 조정중 반복적으로 수행되며, 논문 내에서는 교육을 용이하게 하기 위해 Global Budget Scheduler 를 제안한다.

목표 예산 $b^{(T)}$ 보다 약간 높은 초기 예산 $b^{(0)}$ 에서 시작하며, 증분 행렬의 초기 rank 값을 $r={b^{(0)} \over n}$ 으로 설정한다. 추가로 각 단계 $t_i$ 에 대한 교육을 warm up 한 뒤 $b^{(T)}$ 에 도달할 때까지 예산 $b^{(T)}$ 를 줄이기 위해 cubic schedule 을 따른다. 이러한 방식으로 $t_f$ 단계에 대해 모델을 미세 조정한다.

이러한 방식을 통해 AdaLoRA 는 먼저 매개변수 공간을 탐색한 다음, 나중에는 가장 중요한 가중치에 집중할 수 있다.

 

4. Experiments

이렇게 구현된 AdaLoRA 에 대한 테스트 결과를 보여주는 섹션이다.

표 1: GLUE development set에 대한 DeBERTaV3 기반의 결과. 각 데이터 세트에 대한 최상의 결과는 굵은 글씨로 표시된다. 우리는 STS-B에 대한 평균 상관 관계를 보고한다. 전체 FT, HA 어댑터 및 PA 어댑터는 각각 전체 미세 조정, Houlsby 어댑터 및 Piffer 어댑터를 나타낸다. 우리는 서로 다른 무작위 시드를 사용하여 5번 실행의 평균을 보고한다.

 

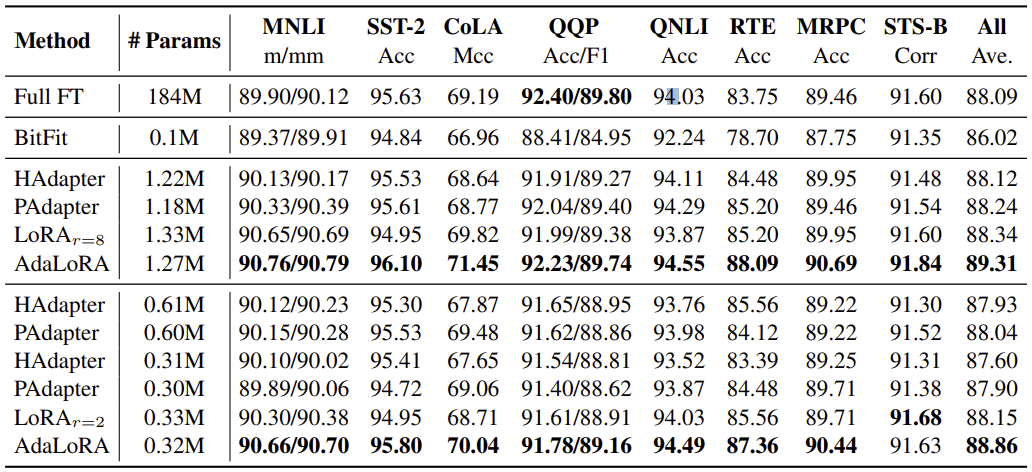
위 표에서 중요한건 Full FT 와 LoRA, 그리고 AdaLoRA 간의 성능 비교이다. 단발적으로 테스트한것이 아닌 무작위 seed 의 5번 실행의 평균을 보고하고 있다. 전반적으로 거의 모든 경우에서 AdaLoRA 가 가장 우수한 결과를 보여주는 모습을 확인할 수 있다.

 

표 2: SQuAD v1.1 및 SQuADv2.0을 기반으로 한 DeBERTaV3 기반 결과. 여기서 #Params는 전체 미세 조정 시와 비교하여 훈련 가능한 매개 변수의 수이다. 우리는 EM/F1을 보고한다. 각 설정에서 최상의 결과는 굵게 표시된다.

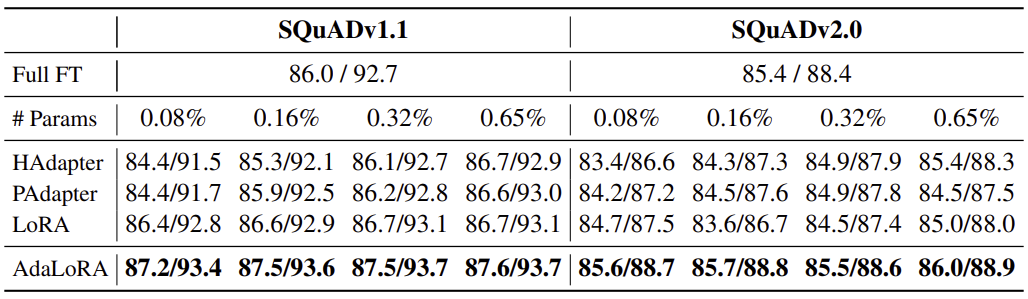
기본적으로 Params 를 늘린다고 극적인 성능변화는 존재하지 않지만, 그래도 미세하게 성능이 상승하긴 한다.

더하여 모든 params 에서 Adapter, LoRA 대비 항상 우수한 성능을 보여준다는 것도 확인할 수 있으며, Fine-Tuning 대비 우수한것도 마찬가지이다.

 

5. 마치며

그림 3: AdaLoRA로 MNLI를 기반으로 DeBERTaV3 기반 미세 조정 시 각 증분 행렬의 결과 순위. 여기서 x축은 레이어 인덱스이고 y축은 다양한 유형의 적응된 가중치 행렬을 나타낸다.

AdaLoRA 는 아마 또다른 혁명이 되지 않을까? 한다. 아쉽게도 나의 수학적인 지식이 부족해 원리를 근본까지 이해하진 못 했지만, 그 효과는 충분히 체감할 수 있었다. 개인적으로 진행하는 연구에 적용해 본 결과, 성능이 Fine-Tuning 은 물론이고 LoRA 를 상회하였으며, 저자들이 논문에서 지나가듯 언급한 '과적합 예방' 효과도 확인해 볼 수 있었다.

전반적으로 Fine-Tuning 대비 성능도 높게 뽑히고, 메모리도 적게 먹고... 대단히 좋은 기술이 아닌가 한다.