해당 포스팅은 PC 환경에 최적화 되어 있습니다.
DeepSeek 라는 중국의 스타트업에서 만든 V3 모델은, OpenAI의 4o 모델에 대응되는 모델로서, 그 성능이 4o와 유사하면서, 추론 비용이 압도적으로 저렴하기에 현재 AI 커뮤니티에서 큰 파장을 불러일으키고 있다.

논문의 Abstract 란에서 바로 벤치마크를 살펴볼 수 있다. Transformer 모델인 만큼 전반적인 벤치마크 수준은 o1, R1 모델 대비 낮지만, 벤치로 식별하기 어려운 창의적인 대화에서는 더 높은 성능을 보여준다.
1. 소개
최근 몇년간 LLM 모델은 진화를 거듭하면서 AGI에 다가가고 있다. 대표적으로 ChatGPT, Claude, LLaMA, Qwen 등을 꼽을 수 있다. 이러한 변화의 물결에 올라, DeepSeek 사는 V3 모델을 제작하였다. V3는 MoE를 기반으로 제작되었으며, 오픈 소스 모델의 한계를 확장하기 위해 제작하였다고 밝히고 있다.
V3 모델을 제작하며 DeepSeek 측에서는 특히 '비용적' 측면에서 모델을 강화하려 노력했다 이를 위해 MLA(Multi-head Latent Attention) 와 학습 비용 절약을 위해 DeepSeekMoE를 채택하고 있다. 이러한 두 아키텍처는 이미 V2 모델에서 검증되었으며, 효율적인 학습과 추론을 달성하면서도 견고한 모델 성능을 유지할 수 있는 능력을 입증했다.

특히
2. 구조
위에서 언급한 MLA와 DeepSeekMoE가 해당 모델에서 특징적인 부분이다.

이미지 좌측 부분에 Transformer Block을 확인할 수 있다. 일반적으로 Transformer Decoder 구조는 아래와 같이 구성된다.

LLM 모델의 경우 일반적으로 Decoder 만 사용되지만, 원론적인 Decoder 구조와 다른 이유는 효율을 위해 DeepSeek 사에서 여러 변형을 거쳐 도출된 구조로 추정된다. V3 모델은 아래와 같이 구성되어 있다.
- RMSNorm → Attention → RMSNorm → Feed-Forward Netwok
- Attention 구조는 MLA
- FFN 구조는 DeepSeekMoE
V3 모델의 핵심은 MLA, DeepSeekMoE 이기에, 해당 구조에 관해서 리뷰한다.
2-1. Multi-head Latent Attention
해당 리뷰를 보고있다면, Attention, Multi-head 같은 기본 지식을 인지하고 있을 것이기에 생략한다.

그렇다면 결국 Latent(잠재) 라는 단어가 남는데, 이 단어가 바로 키 포인트이다. 기본적으로 Attention을 진행할 때 관련성 있는 단어들간의 중요성을 평가하는 과정을 거친다. 이 때 모든시점의 은닉 상태들을 KV(Key-Value) Cache 라는 이름으로 저장하는데, 이 과정에서 매우 많은 메모리를 소모하게 된다. 때문에 DeepSeek 팀에서는 KV 캐시를 작게 압축할 수 있는 방법인 MLA를 적용했다.
- 목적 : KV 캐시 메모리 사용량 감소
- 목적 : 행렬 분해를 통해 계산 효율성 확보
- 목적 : 위치 정보를 명시적으로 인코딩하여 Transformer 고질적 문제 해결
- 효과 : 압축 정보와 위치 정보를 병렬로 활용.
- 즉,
- 효과 : Key-Value 쌍이 동일한 압축 벡터
복잡하게 기술되어 있지만 전체적으로 요약하자면 아래와 같다.
- 입력 압축: 고차원 입력(
- Key 생성 : 압축 Key복원 (2) + RoPE 적용 (3) + 결합 (4)
- Value 생성 : 압축 벡터로부터 직접 복원 (5)
- 결론 : KV 캐시 크기 감소(
더하여, 위 로직과 비슷하게 Attention 의 Query 역시 훈련중 활성 메모리를 줄일 수 있는 low-rank 압축을 수행한다. 전반적으로 KV 와 비슷한 로직이므로 상세한 설명은 생략하겠다.
2-2. DeepSeekMoE
MoE(Mixture of Experts) 는 여러 개의 전문가(expert) 하위 네트워크로 분할하는 신경망의 아키텍처 패턴으로서, 처음 해당 구조를 들엇을 때는 Attention에 사용될 것이라 예상했는데, V3 모델에 사용된 MoE는 FFN 레이어에서 사용된다.
For Feed-Forward Networks (FFNs), DeepSeek-V3 employs the DeepSeekMoE architecture (Dai et al., 2024)
V3에 사용된 DeepSeekMoE는 전통적인 MoE 기법인 GShard 와는 다르게, 세분화된 전문가들을 사용하며 일부 전문가들을 공유해서 사용한다.
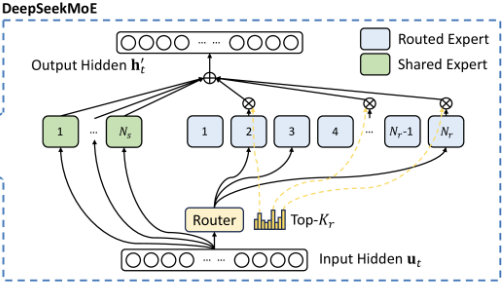
아래 수식은,
상세하게 설명하자면 아래와 같다.
최종적으로 정리하자면, DeepSeekMoE는 공유 전문가, 라우팅 전문가를 사용하여 입력 토큰에 따라 다른 전문가를 선택하는 방식으로, 이 선택과정은 유사도 점수를 기반으로 상위
외에도 논문에서는 적용된 여러 기법들에 대해서 설명하고 있다. 하지만 핵심적인 기법은 MLA와 DeepSeekMoE 기법이기에 나머지 기법들에 대해선 생략한다.
2-3. FP8
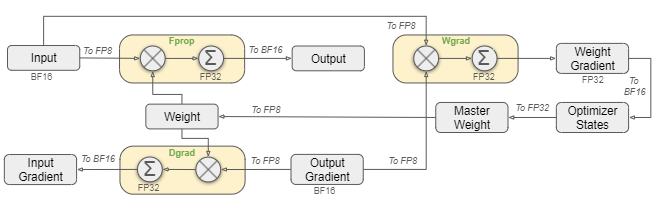
해당 모델은 여러 버전으로 배포된 것으로 보인다. HuggingFace 에서 Tensor type 이 아래와 같기 때문이다.

일반적으로 BF16 를 사용하는데, 해당 모델에서는 FP8을 사용하면서도 BF16대비 손실오차 0.25% 이하로 유지하는데 성공하였다. 즉, 성능하락은 체감하기 어려운 반면, 메모리 소모량은 크게 줄일 수 있는 방법을 적용하였다.
3. 결론
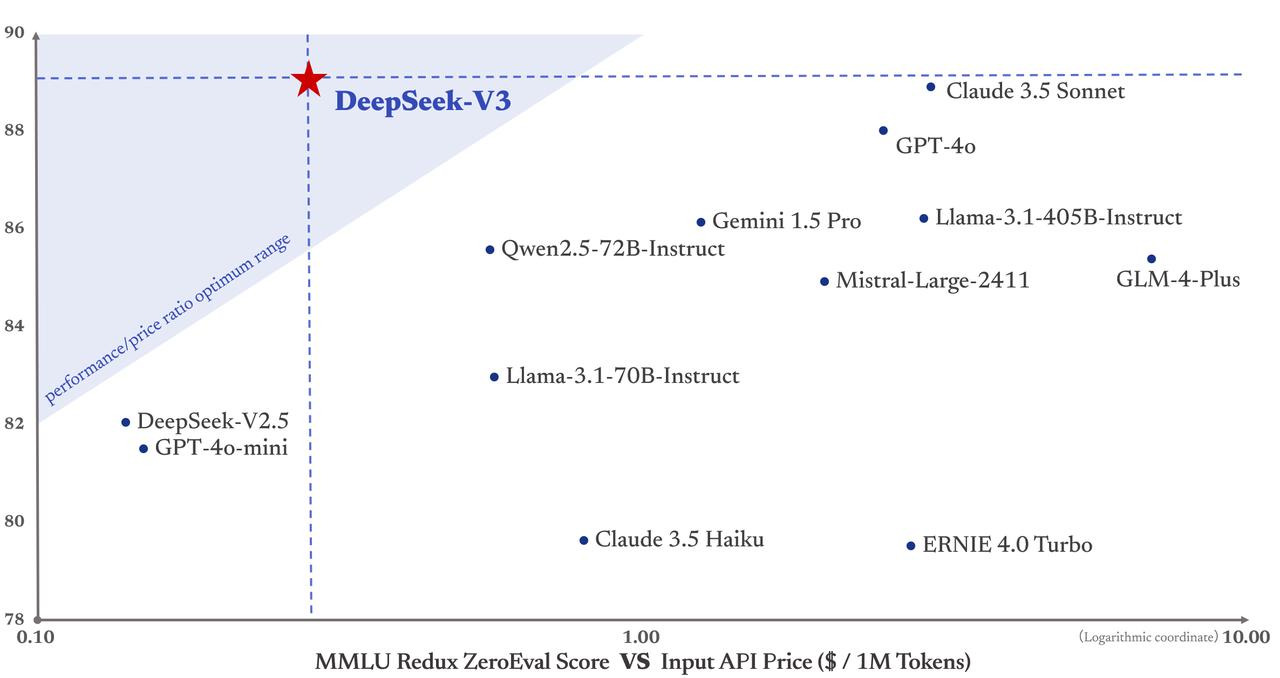
DeepSeek V3는 그 성능도 최고 수준이지만, 가장 무서운 점은 '압도적인 가성비' 이다.(여기서 말하는 가성비는 '추론' 가성비라 위에서 언급한 의심쩍은 '훈련' 비용과는 다르다.) 많은 사람들이 중국 제품에 대해 안전하지 못하다는 감정을 느끼면서도 중국 제품을 찾는 이유는 '가성비' 이다. 개인적으로 생각하기에도 3배 이상 저렴하다면, 일상적인 용도로 DeepSeek 제품을 충분히 권장할만 하다.(오히려 권장하지 않는다는게 문제라는 생각이다.)
한편으로 느끼는 궁금증은 다른 AI 제조사들의 비싼 비용이다. 내가 알기론, 이미 ChatGPT도 MoE를 사용하고 있으며, 추가로 많은 최적화 기법들이 고려되었을 것이다. 하지만 4o는 V3 보다 3배 비싸며, o1은 R1 보다 27배 더 비싸다.
논문을 읽어보면서 느끼길, 논문의 내용을 내가 구현하기에는 무리가 있는 레벨이지만, 결코 OpenAI 가 구현하기에 버거울 수준의 내용은 아니라고 판단했다. 하지만 DeepSeek는 구현했고, OpenAI는 현재까지 구현하지 못했다. 조만간 2주내로 o3, o3-mini 모델이 공개될 예정인데... 잘 나와서 LLM 기술에서 경쟁이 활발해지길 바란다.
